无向图三元环计数
计算每个点的度数,后将无向边变为有向边,从度数大的点连向度数小的点,如果度数相同则从编号大的点连向编号小的点。
然后我们需要统计的环变成了如下的形式:
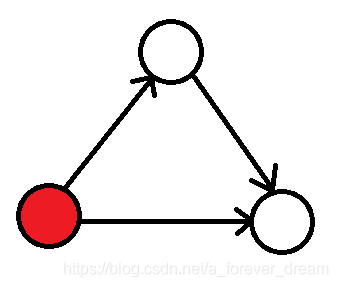
每个三元环当且仅当统计到红点时被统计上。
现在算法步骤如下:
枚举每个点 $v$。
对于点 $v$,将其出边所连的点打上临时标记。
枚举 $v$ 的每个出点的出点,如果该点亦被打上标记,说明找到三元环,直接累积答案即可。
关于这个算法的时间复杂度。
对于每一条边 $x \rightarrow y$,改边被遍历的次数为 $\deg _ { in} (x)$,那么时间复杂度就是 $ O(\sum _ {(x , y) \in E} \deg _ { in } (x)) $。
因为每个连向 $x$ 的点的度数都大于 $\deg _ { in } (x)$,也就是说至少有 $\deg _ {in} (x)$ 个点的点度大于 $\deg _ {in} (x)$,那么就至少存在 $\deg _ { in } (x) ^ 2$ 条边。
而我们又知道必然有 $\deg _ { in } (x) ^ 2 \le m$,所以说 $\deg _ { in } (x) \le \sqrt{m}$。
所以我们最后的复杂度就是 $O(m\sqrt{m})$ 的。
对于四元环计数,我们采取类似的方法,先变成有向图,然后再把四元环分为两类来计数。
不过是多了一些讨论的枚举。
复杂度玄学,只会口胡/qd。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
namespace Ehnaev{
inline ll read() {
ll ret=0,f=1;char ch=getchar();
while(ch<48||ch>57) {if(ch==45) f=-f;ch=getchar();}
while(ch>=48&&ch<=57) {ret=(ret<<3)+(ret<<1)+ch-48;ch=getchar();}
return ret*f;
}
inline void write(ll x) {
static char buf[22];static ll len=-1;
if(x>=0) {do{buf[++len]=x%10+48;x/=10;}while(x);}
else {putchar(45);do{buf[++len]=-(x%10)+48;x/=10;}while(x);}
while(len>=0) putchar(buf[len--]);
}
}using Ehnaev::read;using Ehnaev::write;
const ll N=1e5,M=2e5;
ll n,m,tot;
ll deg[N+5],u[M+5],v[M+5],flg[N+5];
ll head[N+5],nxt[M+5],ver[M+5];
inline void Addedge(ll u,ll v) {
ver[++tot]=v;nxt[tot]=head[u];head[u]=tot;
}
int main() {
n=read();m=read();
for(ll i=1;i<=m;i++) {
u[i]=read();v[i]=read();if(u[i]<v[i]) swap(u[i],v[i]);
deg[v[i]]++;deg[u[i]]++;
}
for(ll i=1;i<=m;i++) {
if(deg[v[i]]>deg[u[i]]) Addedge(v[i],u[i]);
else Addedge(u[i],v[i]);
}
ll ans=0;
for(ll v=1;v<=n;v++) {
for(ll i=head[v];i;i=nxt[i]) {flg[ver[i]]=1;}
for(ll i=head[v];i;i=nxt[i]) {
for(ll j=head[ver[i]];j;j=nxt[j]) {if(flg[ver[j]]) ans++;}
}
for(ll i=head[v];i;i=nxt[i]) {flg[ver[i]]=0;}
}
write(ans);
return 0;
}
|
