P4718

发表于 分类于
【模板】Pollard-Rho算法

【模板】Pollard-Rho算法

实际上是 Pollard-Rho 和 Miller-Rabin 的缝合模板题。

首先关于 Miller-Rabin 素性测试。

很多关于这方面的数学上的解释我现在做不来，所以只能记录一下使用。。。

费马素性测试：如果对于 $a \in ( 1 , p ) $，存在 $a ^ { p - 1 } \not \equiv 1 \pmod { p } $，则 $p$ 一定不是一个素数；反之，若有若干个 $a$ 满足 $a ^ { p - 1 } \equiv 1 \pmod{p}$，则 $p$ 大概率是素数。

因此我们随机几个 $a$ 来测试素性。

这是个很玄学的方法，正确性的保证不高。

有的合数也能满足 $\forall a \in (1,p) , a ^ { p - 1 } \equiv 1 \pmod {p}$，被称为卡迈尔数，或者费马伪素数。

$561 = 3 \times 11 \times 17$ 就是一个卡迈尔数，并且若 $n$ 是一个卡迈尔数，则 $m = 2 ^ n - 1$ 也是一个卡迈尔数，即其个数是无穷的。最重要的是在 $10 ^ 9$ 内，这样的合数有 $646$ 个，想拿这个混作正经素性测试还是省省吧。

于是我们需要考虑优化这个素性测试。

二次探测定理：若 $p$ 为奇素数，则 $x ^ 2 \equiv 1 \pmod { p }$ 的解为 $x \equiv \pm 1 \pmod{ p }$。

我们以原本的费马素性测试作为依托，如果 $a ^ { p - 1 } \equiv 1 \pmod{p}$ 不成立的话，直接判为合数即可；反之我们尝试使用二次探测定理继续判断。

至于如何使用二次探测定理继续判断，我们先将 $p-1$ 分解为 $p - 1 = d \times 2 ^ {r}$，其中 $d$ 是一个奇数。

首先如果 $a ^ d \equiv \pm 1 \pmod { p }$，这是满足二次探测定理的，我们认为其通过了这次子测试。

反之我们尝试将 $d$ 不断乘 $2$（实际操作中将 $a ^ d$ 进行平方），最多乘 $r - 1$ 次，如果说存在 $a ^ d \equiv - 1 \pmod { p }$，我们也认为其通过了这次子测试（不可能等于 $1$ 的，不然最开始的 $a ^ d$ 一定是 $1$）。

反之说明其没有通过本次子测试，一定是个合数。

我们设 $x = a ^ { ( p - 1) / 2 } $，实际上这个过程就是说明 $x ^ 2 \equiv 1 \pmod { p }$ 的解是 $x \equiv \pm 1 \pmod { p }$，满足二次探测定理，而如果没有通过子测试，说明 $x \not \equiv \pm 1 \pmod { p }$，这是违背二次探测定理的，说明 $p$ 一定不是奇素数。

这种通过二次探测定理优化的素性测试即 Miller-Rabin 素性测试。

实际操作中，我们随机不少于 8 次 $a$，比如 10 次。这样既保证正确率比较高，也不会过于影响效率。

当然，在 OI 的环境下，数字一般是 $2 ^ { 6 4 }$ 以内的，我们实际上可以通过选取固定的 $a$ 来实现快速的确定性判素。

  • 对于 $2 ^ { 3 2 }$ 以内判素，选取 $2,7,61$ 三个数即可。
  • 对于 $2 ^ { 6 4 }$ 以内判素，选取 $2,325,9375,28178,450775,9780504,1795265022$ 七个数即可。
  • 在考场上，出于这些数字的背诵没什么必要，我们用前十二个质数（到 $37$）即可实现 $2 ^ { 7 8 }$ 确定性判素。

至于原理，我完全不知道，但是感性理解应该并不难吧？

测试一次的复杂度是 $O( k \log ^ 3 p)$ 的。其中 $k$ 是测试轮数。

Pollard-Rho 是一个更玄学的东西，可以在期望 $O( n ^ {1 / 4})$ 的复杂度下求出 $n$ 的一个非平凡因子。所谓非平凡因子，就是 $( 1 , n )$ 内的一个 $n$ 的因子。

我们先构造伪随机数：令 $f(x)= (x ^ 2 + c ) \bmod n$，其中 $c$ 是一个随机常数。

然后初始随机取一个 $x _ 1$，其后每次 $x _ i = f ( x _ { i - 1 })$。

这个伪随机数是有循环节的，类似下面的图。

rho

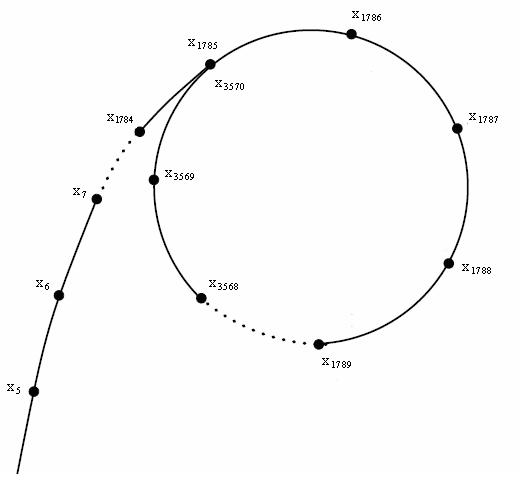
长得很像 $\rho$，所以叫做 Pollard-Rho（所以按理说这个 Rho 应该小写吗？）。

根据生日悖论，这个环和尾的期望长度都是 $O( \sqrt {n})$ 的。

在这一堆随机数中，我们尝试选取 $x _ i $ 和 $x _ j $ 构造 $| x _ i - x _ j |$，通过 $\gcd ( | x _ i - x _ j | , n)$ 来找到 $n$ 的一个非平凡因子。由于某些神奇的原因，在这种优秀的随机数列下，我们能在期望下 $O( n ^ {1 / 4})$ 的复杂度下找到这样的因子。

有一种 Floyd 判环的方法，其方法就是使 $a = f ( a )$ 单次迭代，而 $ b = f ( f ( b ))$ 二重迭代，造成二者的差距，从而构造出 $x _ i $ 和 $x _ j$。其间若发现成环（就是 $a$ 和 $b$ 相等了），直接退出即可。反之若发现平凡因子，直接返回即可。

但是这种实现下，$\gcd$ 的调用次数很多，因此我们通过倍增优化来减少调用 $\gcd$ 的次数。

具体来说，我们每次固定下 $x _ i$，然后倍增式多次迭代 $x _ j$（第一次迭代 1 次，第二次 2 次，第三次 4 次，以此类推），并令 $s = \prod | x _ i - x _ j | $，一旦 $s = 0$ 说明分解失败，返回 $n$（下一次再用 Pollard-Rho 尝试分解，直到分解出来，因为经过 Miller-Rabin 之后我们判断这个数肯定不是素数）。

过程中，每隔 $2 ^ k - 1$ 个数就查询一次 $\gcd$。这里取 $k=7$。

对于本题找最大质因子的需求，不断分解并判素即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<ctime>
#define ll __int128
using namespace std;
namespace Ehnaev{
  inline ll read() {
    ll ret=0,f=1;char ch=getchar();
    while(ch<48||ch>57) {if(ch==45) f=-f;ch=getchar();}
    while(ch>=48&&ch<=57) {ret=(ret<<3)+(ret<<1)+ch-48;ch=getchar();}
    return ret*f;
  }
  inline void write(ll x) {
    static char buf[22];static ll len=-1;
    if(x>=0) {do{buf[++len]=x%10+48;x/=10;}while(x);}
    else {putchar(45);do{buf[++len]=-(x%10)+48;x/=10;}while(x);}
    while(len>=0) putchar(buf[len--]);
  }
}using Ehnaev::read;using Ehnaev::write;
inline void writeln(ll x) {write(x);putchar(10);}

ll T,max_factor,n;
ll test_mr[13]={2,3,5,7,11,13,17,19,23,29,31,37};

inline ll gcd(ll a,ll b) {return b==0?a:gcd(b,a%b);}

inline ll Pow(ll b,ll p,ll mo) {
  ll r=1;while(p) {if(p&1) r=r*b%mo;b=b*b%mo;p>>=1;}return r;
}

inline ll Abs(ll x) {return x>=0?x:-x;}

inline bool Miller_Rabin(ll p) {
  if(p<2) return 0;if(p==2||p==3) return 1;
  ll d=p-1,r=0;while(!(d&1)) {r++;d>>=1;}
  for(ll k=0;k<12;k++) {
    ll a=test_mr[k]%p;if(a==0) continue;
    ll x=Pow(a,d,p);if(x==1||x==p-1) continue;
    for(ll i=0;i<r-1;i++) {x=x*x%p;if(x==p-1) break;}
    if(x!=p-1) return 0;
  }
  return 1;
}

inline ll Pollard_Rho(ll x) {
  ll s=0,t=0;ll c=rand()%(x-1)+1;ll step=0,goal=1;ll val=1;
  for(goal=1;;goal<<=1,s=t,val=1) {
    for(step=1;step<=goal;step++) {
      t=(t*t+c)%x;val=val*Abs(t-s)%x;
      if(step%127==0) {ll d=gcd(val,x);if(d>1) return d;}
    }
    ll d=gcd(val,x);if(d>1) return d;
  }
}

inline void Fac(ll x) {
  if(x<=max_factor||x<2) return;
  if(Miller_Rabin(x)) {max_factor=max(max_factor,x);return;}
  ll p=x;while(p>=x) p=Pollard_Rho(x);
  while(x%p==0) x/=p;Fac(x);Fac(p);
}

int main() {

  T=read();

  while(T--) {
    srand((unsigned)time(0));
    max_factor=0;n=read();Fac(n);
    if(max_factor==n) printf("Prime\n");
    else writeln(max_factor);
  }

  return 0;
}