Geometry
这里把大部分板子都放过来了。
除了三维计算几何和圆反演的内容(这两块恐怕要等我上大学之后)。。。
讲的会比较简略,可能会把 Whk 的内容搬过来。
然后告诫一句:这个东西 OI 基本考不到,花太多时间在上面是不值得的。。。
为什么我会写这个东西?无聊而已。。。而且我想多学一点东西,不仅仅是为了做题。
这些东西都是《算法竞赛入门到进阶》上的,一部分是杜老师的,反正都是干货(毕竟在 OI 里似乎没有什么讲头,而且非常码农)。
那张闵可夫斯基和的图片是 shadowice1984 的。
要注明的话东西比较多,又不是写论文,所以我就懒了 QAQ。
Luogu 只有三道模板,二维凸包、旋转卡壳和半平面交。三维的还有一部分模板但我不会。。。想要测模板可以自己去交。。。
一个事情就是这里的大部分模板没有测过(除了上述模板题以及其相关的函数),所以很有可能有锅 QAQ,但我也懒得对拍了,所以非常抱歉,对拍就咕了。
例题会补上的(咕咕咕)。
一、常数定义
eps 用来保证精度,Pi 后面会用。
代码:
1 | // Some cosntant. |
二、Sgn 和 Cmp 函数
为了方便保证精度写的函数。
代码:
1 | // The Sgn function & Cmp function. |
三、点与向量
点可以表示向量,所以就不 typedef 了。
代码:
1 | // Point & Vector. |
四、计算两点间距离
勾股定理。。。
代码:
1 | // To calculate the distance of two Points. |
五、向量点积类操作
坐标下的点积运算不用说了吧?
$$\begin{aligned}\mathbf{a}\cdot\mathbf{b} & =|\mathbf{a}||\mathbf{b}|\cos \theta\\ &=(x_a,y_a)\cdot(x_b,y_b)\\ &= x_ax_b-y_ay_b\end {aligned}$$
可以用这个判断垂直(以及夹角的锐钝),计算夹角,通过平方还可以计算向量长度。
实际上就是:
$$\mathbf{a}\cdot\mathbf{b}=0\Leftrightarrow \mathbf{a}\perp \mathbf{b}$$
$$\cos \theta =\dfrac{\mathbf{a\cdot b}}{|\mathbf{a}||\mathbf{b}|}$$
$$|\mathbf{a}|=\sqrt{\mathbf{a^2}}$$
然后就是表示运算的这个点($\cdot$)是不能省略的。
1 | // Dot product. |
六、向量叉积类操作
叉积众所周知:
$$\begin{aligned}\mathbf{a}\times \mathbf{b}&= |\mathbf{a}||\mathbf{b}|\sin \theta\\ &= (x_a,y_a)\times (x_b,y_b)\\ &= x_ay_b-x_by_a\end{aligned}$$
这个东西的功用多一点,可以算两个向量所夹的平行四边形的面积(就是叉积值,所以下面那个函数表示求一个三角形的面积的两倍,但是一般情况下这个值是有正负的,表示顺时针还是逆时针),还可以判断平行之类的(叉积值等于 0)。
一些 Trivial 的操作一并附在下面了,就顺带讲掉。
一个是将向量旋转 $\theta$。
众所周知啊,复数相乘在复平面上表现为模长相乘,辅角相加。
设向量 $\mathbf{a}=x+yi$,那么旋转 $\theta$ 相当于乘上一个单位向量 $\mathbf{e}$,其辅角为 $\theta$,显然 $\mathbf{e}=\cos \theta+i\sin\theta$。
那么就有:
$$\begin{aligned}\mathbf{a}\times \mathbf{e}&=(x+yi)(\cos \theta+i\sin\theta)\\&=x\cos\theta-y\sin\theta+(x\sin\theta+y\cos\theta)i\end{aligned}$$
坐标不用我讲了吧?
以及一个求法向量的操作,其实就是将向量逆时针旋转 $\dfrac{\pi}{2}$,然后再变成单位向量即可。
逆时针旋转 $\dfrac{\pi}{2}$ 即:
$$(x,y)\rightarrow(-y,x)$$
代码:
1 | // Cross product. |
七、直线与线段
这一块的东西巨大多繁琐。
定义结构体中的直线由两个点表示(在后面半平面的表示中含义会有所不同),不需要极角序的话可以不用记录角度。结构体中后面的几个析构函数分别是将点角表示和解析式表示转化为两点表示,最后的重载运算符是为了极角排序用的。
点与直线的关系,用叉积正负判断是在直线逆时针方向还是在顺时针方向还是在直线上。
点与线段的关系。首先根据叉积判断点在直线上,再根据点积正负判断点在线段上。
点与直线的距离,就是高的长度。其实就是构造一个平行四边形然后除以高。因为有正负之分所以取绝对值。
然后是点到线段的投影(因为是点所以最后还要加上起点)。实际上就是:
$$\begin{aligned}|\mathbf{a}|\cos\theta\mathbf{e}&=|\mathbf{a}|\dfrac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{a}||\mathbf{b}|}\cdot\dfrac{\mathbf{b}}{|\mathbf{b}|}\\&= \dfrac{\mathbf{a}\cdot\mathbf{b}}{\mathbf{b}^2}\cdot\mathbf{b}\end{aligned}$$
点关于直线的对称点。先求投影向量得到一个平行四边形,利用其对角线与边的加减的到对称点的向量表示。
点与线段的距离。实际上就是分类讨论一下,如果就是高的话直接求即可,反之取到两端点的距离的最小值即可。是否是高根据点积来得到夹角的钝锐性判断。
直线之间的关系,先判断叉积是否为 0(这样的话不是平行就是重合,根据点是否在直线上判断即可),反之肯定是相交。
求直线交点。可以联立求解,这里将一个几何方法:
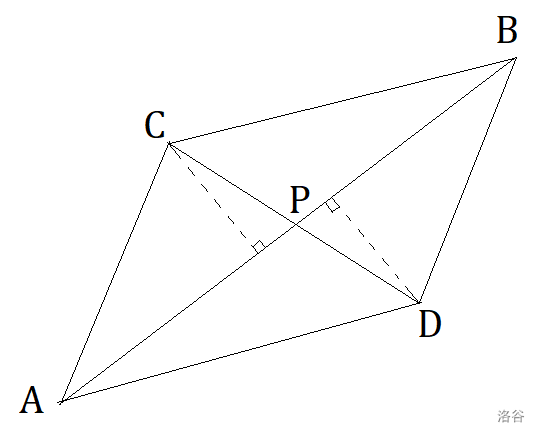
图中有直线 $AB$ 与 $CD$ 交于点 $P$,根据这个面积、底与高的简单关系和相似可知:
$$\dfrac{DP}{CP}=\dfrac{S_{\triangle ABD}}{S_{\triangle ABC}}=\dfrac{\overrightarrow{AD}\times\overrightarrow{AB}}{\overrightarrow{AB}\times\overrightarrow{AC}}=\dfrac{x_D-x_P}{x_P-x_C}=\dfrac{y_D-y_P}{y_P-y_C}$$
简单变换一下就成了:
$$x_P=\dfrac{S_{\triangle ABD}x_C+S_{\triangle ABC}x_D}{S_{\triangle ABD}+S_{\triangle{ABC}}}$$
$$y_P=\dfrac{S_{\triangle ABD}y_C+S_{\triangle ABC}y_D}{S_{\triangle ABD}+S_{\triangle ABC}}$$
面积显然可以叉积求,这个东西的比值显然可以被叉积之间互相消掉,细节就不讲了。
当然因为这里有做除法的危险操作,如果题目没有说明三点共线的情况不存在一定要特判!!!
线段相交。判断对于每一条线段,另外一条线段的两个点是否分别在这条线段的顺时针和逆时针方向。
线段交点。先判断是否相交,再判断直线交点。
代码:
1 | // Line. |
八、多边形
判断一个点是否在多边形内部。
有一种方法是从该点引出一条射线,然后判断射线与多边形的边相交的次数,奇数次说明在多边形内部,偶数次说明在外部。
另一种方法是转角法,每个点连接,然后绕多边形一周计算转角,如果说在转过 $2\pi$ 说明在内部,$\pi$ 说明在边界上。但是使用反三角函数会有精度问题。
我们利用转角法的思想,换一种实现方式。与每一条边检查如下的东西:
$$c=Cross(P-j,i-j)$$
$$u=i.y-P.y$$
$$v=j.y-P.y$$
根据 $u$,$v$ 检查过 $P$ 的水平线是否经过该边,根据 $c$ 判断是在顺时针方向还是在逆时针方向。
然后我们用一个 $num$ 来计数,若 $num>0$ 说明在内部;否则在外部(在边上可以单独判断)。这里具体看代码。我不太能解释,但是感性理解就是对的(确信)。
求多边形面积。叉积啥的可以相互抵消,所以实际上这个面积就是以原点做三角剖分,再把叉积加起来除以二(因为叉积的值是三角形面积值的两倍)。
求多边形重心。给多边形作三角剖分,按照三角形的有向面积求加权平均,然后就能求出重心(然而我也不知道什么原理)。
代码:
1 | // Polygon. |
九、二维凸包
这里介绍 Graham 扫描法的变种 Andrew 算法。
算法做两次扫描,先从最左边的点沿“下凸包”扫描到最右边,再从最右边的点沿“上凸包”扫描到最左边,两个凸包合起来就是完整的凸包。
然后,按照横坐标从小到大排序,然后按照这个拐弯来判断凸包,实际上还是挺朴素的。
代码:
1 | // Convex hull. |
十、最近点对
代码:
1 | // Closest pair. |
十一、旋转卡壳
先求凸包。
这个东西可以求凸包直径。
用两条平行线卡住凸包,然后旋转旋转。
代码:
1 | // Rotating calipers. |
十二、半平面交
向量逆时针方向可以表示一个半平面。
所以可以直接用一个点表示向量经过这个点,再用一个向量表示方向。
然后极角排序,双端队列扫描半平面,最后能得到半平面交出的多边形。
时间复杂度 $O(n\log n)$。
然后注意一下这个交点不是原来的函数了,因为半平面的表示方法不一样。
代码:
1 | // Half plane intersection. |
十三、圆
圆的结构体定义一个圆心的位置和一个半径。
点或线与圆的关系很简单。。。求个距离与半径比较就完了。
然后是直线与圆的交点,根据圆心到直线距离得到弦长,然后还能确定方向和直线的单位向量,从而得到了两个点的坐标。
代码:
1 | // Circle. |
十四、最小圆覆盖
不会几何法,所以,模拟退火!!!(但是没有用随机)
但我也不知道没有用随机是否能满足一般的高斯正态分布。。。
代码:
1 | // Minimum Cover Circle. |
十五、闵可夫斯基和
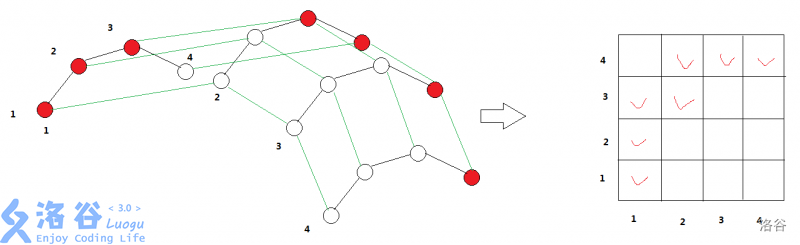
求出 $p$,$q$ 凸壳,然后用双指针合并。
简单来说走 $n+m-1$ 步,然后借助斜率选择凸壳上的点。
代码:
1 | // Minkowski Sum. |
十六、模板集合
终于写完了,这边把几何模板合在一起放在这里。
代码:
1 |
|